When generating random positions and orientations that are to be used to test an image registration algorithm, it is very important that he distribution of the orientations is truly uniform, i.e. all orientations should be equally represented by the distribution. If this is not the case, then some orientations will be under-represented in the simulation while others are over-represented.
Concepts
To start, we have to choose a way to express the orientation. The most convenient is to express the orientation as a rotation about a unit vector, since it is easy to convert an orientation that is expressed in this way into either a quaternion or into three Euler angles. In order for this vector/rotation representation to provide uniform orientations, two things must be true:
- The vector orientation must be such that, if the vector is placed in a unit sphere, it must be equally likely to point to any location on the surface of one hemisphere of the unit sphere.
- The rotation around the vector must be uniformly distributed over the range
![[-pi,+ pi]](/mw/images/math/8/6/8/868b20e4d06740a47d34b774131c6392.png) .
.
The reason that we only need one hemisphere is that any orientation can be equally represented either as a rotation about a vector, or as a rotation in the opposite direction about a vector that points in the opposite direction. In other words, since the rotation around the vector to be positive or negative, we don”t need vectors that point in the opposite direction.
Specifics, With Rotation Angles
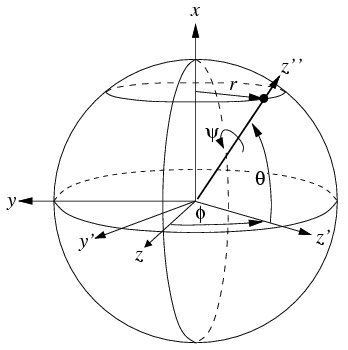
The diagram on the right shows both the unit sphere and a set of roll, pitch, yaw 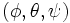 angles that represent an orientation. The angles
angles that represent an orientation. The angles  and
and  are used to set the orientation of the vector, while
are used to set the orientation of the vector, while 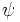 is the rotation around the vector (specifically, it is around the new
is the rotation around the vector (specifically, it is around the new 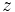 axis after the other
axis after the other
two rotations have taken place).
The probability of any particular vector orientation must be uniformly distributed, in other words,
the probability of the vector intersecting a unit area 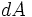 at a point on the sphere
at a point on the sphere
must be the same everywhere on the sphere. In order to achieve this, the probability of the vector
intersecting a ring at elevation 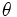 (see diagram) must be proportional to the
(see diagram) must be proportional to the
circumference of that ring. Noting that the circumference is proportional to the radius
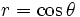 of the ring, we can show that the probability must be proportional
of the ring, we can show that the probability must be proportional
to 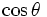 .
.
In other words, we want 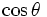 , rather than
, rather than 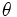 itself, to follow
itself, to follow
a uniform distribution. If we were to simply generate 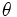 as a uniform random number,
as a uniform random number,
then the probability of an orientations near the pole would be much higher than near the equator.
So we can state the probability distributions for angles 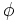 and
and 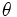
as follows:
![p(phi) = a qquadqquad mbox{where} qquad phi in [0,2pi]](/mw/images/math/2/3/7/23710671e4f538af1967a2c8f303152a.png)
![p(theta) = b,cos(theta), quad mbox{where} qquad theta in [0,pi/2]](/mw/images/math/f/a/f/faf57676ff5c1c1d2988285342de752f.png)
The actual magnitude of the rotation is determined solely by the third angle 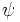 ,
,
so if we want a uniform distribution of rotations up to magnitude 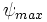 .
.
![p(psi) = c qquadqquad mbox{where} qquad psi in [-psi_{max},psi_{max}]](/mw/images/math/1/1/2/112c4453983a86fc356d20e3f658b024.png)
The random number generators that we use will generate uniform random number in the range [0,1] which we must then
use to generate the probability distributions shown above. We will need three such random numbers: 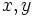 and
and 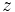 .
.
Generating random values for 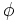 and
and 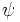 is easy since these are uniformly distributed, we can just use the following:
is easy since these are uniformly distributed, we can just use the following:
![phi = 2pi, x qquadqquadqquad mbox{where} qquad x in [0,1]](/mw/images/math/d/3/7/d374deaf0db1063d7daee46aae7d1b58.png)
![psi = psi_{max}, (2, z - 1) qquad mbox{where} qquad z in [0,1]](/mw/images/math/7/4/d/74d1dbbf06d98a8e4c3fa6a458df161f.png)
Generating random values for 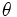 requires what is called the
requires what is called the
“inverse transform method,”
which states that the relation between a probability distribution 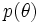 and a uniform random variable
and a uniform random variable 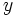 is given by the following:
is given by the following:
![int_{theta_{min}}^{theta} p(theta') , dtheta' = y qquad mbox{where} qquad y in [0,1]](/mw/images/math/5/d/3/5d395a6c76cb7d95b2a468063f698ba7.png)
All we have to do is solve the above equation for 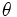 , and we have the answer we need. Substituting our probability function gives
, and we have the answer we need. Substituting our probability function gives
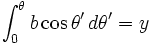
where 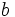 is just a constant that ensures that the integral of the probability over all values is unity, i.e.
is just a constant that ensures that the integral of the probability over all values is unity, i.e.
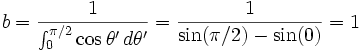
Substituting 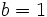 and solving the integral, we get
and solving the integral, we get
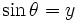
Solving for 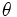 , we have our final answer:
, we have our final answer:
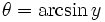
Final Result
To generate a uniformly random orientation, use the orientation angles that are specified above and use the following equations to generate the angles from three uniform random numbers 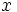 ,
, 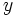 and
and 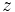 :
:
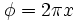
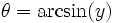
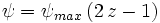
Note that 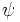 does not necessarily have to follow a uniform distribution
does not necessarily have to follow a uniform distribution ![[-psi_{max}, +psi_{max}]](/mw/images/math/b/e/9/be9d65c86452681badc90ee226c5184c.png) , we could also use a gaussian distribution or whatever other distribution we may desire.
, we could also use a gaussian distribution or whatever other distribution we may desire.
Given the orientation angles, the next step is generate a rotation matrix:
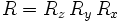
where 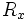 is a rotation by
is a rotation by 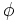 about the
about the 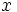 axis,
axis, 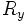 is a rotation by
is a rotation by 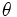 about the
about the 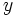 axis, and
axis, and 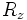 is a rotation by
is a rotation by 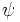 about the
about the
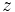 axis.
axis.
If you use a different convention for expressing orientations, then you can perform a similar derivation by utilizing the concept of uniform coverage of a unit sphere. The answer you get should be very similar to what is shown here, where two of the angles follow uniform distributions and one angle follows either a sin or cos distribution, depending on how the rotations are defined.